การหางานจากพื้นที่ใต้กราฟ

ในบางสถานการณ์วัตถุถูกแรงกระทำไม่คงที่ ทำให้งานที่ได้มีค่าไม่แน่นอน แต่เราก็สามารถประมาณงานที่เกิดขึ้นได้โดยใช้กราฟช่วย ดังนี้

เนื้อหา :

1. หางานจากกราฟในกรณีที่แรงมีขนาดคงที่

การหางานจากพื้นที่ใต้กราฟกรณีแรงคงที่ — หาปริมาณงานเนื่องจากแรงคงที่

จากสมการงาน $Work = F \times D$ และเทียบกับกราฟด้านบน เราจะเห็นได้ว่า งานที่เกิดขึ้นจะมีค่าเท่ากับพื้นที่ใต้กราฟของแรง หรือพื้นที่สีเหลือง

$Work_1 = F \times D = Yellow Area = Width \times Height$

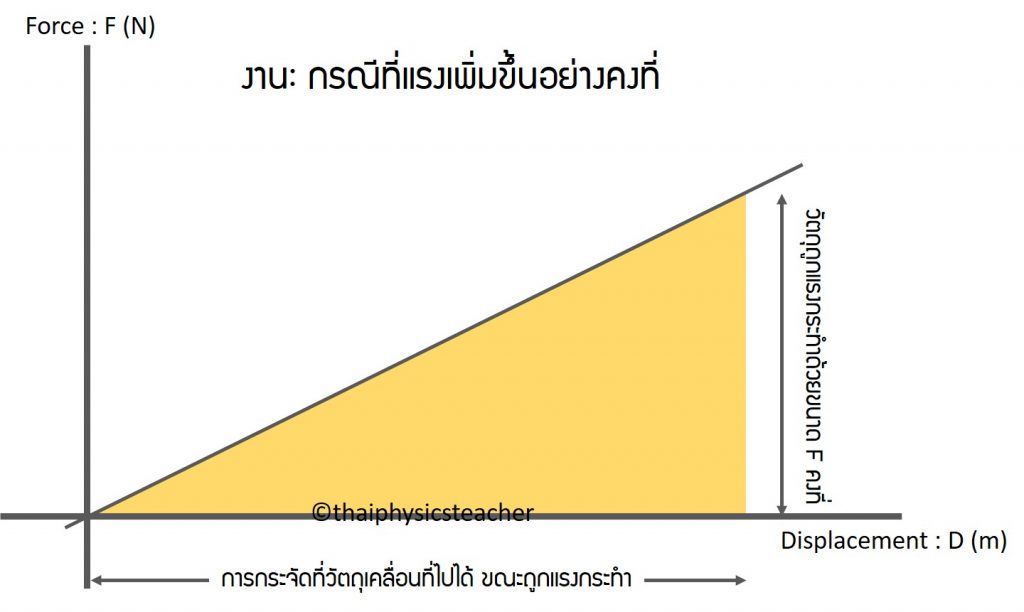
2. หางานจากกราฟในกรณีที่แรงมีขนาดเพิ่มขึ้นอย่างคงที่

การหางานจากพื้นที่ใต้กราฟ — งานกรณีแรงมีขนาดเพิ่มขึ้นอย่างคงที่

แต่เมื่อไหร่ก็ตามที่วัตถุถูกแรงกระทำที่มีขนาดเพิ่มขึ้นอย่างคงที่ (หรือลดลงอย่างคงที่ก็ได้เช่นกัน) งานที่ได้จะมีขนาดครึ่งหนึ่งของกรณีที่ 1 หรือ เราสามารถพิจารณาเป็นพื้นที่สามเหลี่ยมสีเหลือง ก็ได้เช่นกัน ดังนี้

$Work_2 = \frac{1}{2} \times F \times D = Yellow Area = \frac{1}{2} \times Width \times Height$

3. หางานจากในกรณีที่แรงมีขนาดไม่คงที่

การหางานจากพื้นที่ใต้กราฟ ฟิสิกส์ — งานกรณีแรงมีขนาดไม่คงที่

ในสถานการณ์จริง แรงที่กระทำกับวัตถุมักมีค่าคลาดเคลื่อนและไม่สม่ำเสมอ ยกตัวอย่างเช่นกราฟด้านบน แต่เราก็สามารถหางานได้โดยการสร้างรูปสี่เหลี่ยมผืนผ้าที่มีความกว้าง $\Delta{D}$ โดยซอยบนพื้นที่สีเหลืองทั้งหมด ส่วนความสูงก็คือแรง $F_i | i = 1, 2, 3, ..., n$ จะทำให้งานรวมที่เกิดขึ้น = งานย่อยๆที่เกิดจากผลรวมพื้นที่สี่เหลี่ยมผืนผ้าสีขาว ดังสมการนี้

$W_{total} = W_1 + W_2 + W_3 + ... + W_n$

$W_{total} = (F_1)(\Delta{D}) + (F_2)(\Delta{D}) + (F_3)(\Delta{D}) + ... + (F_n)(\Delta{D})$

ดึงตัวร่วม $\Delta{D}$ ออกมา จะได้

$W_{total} = (F_1 + F_2 + F_3 + ... + F_n)(\Delta{D}) --- (1)$

แต่เนื่องจากเทอม $\Delta{D}$ เป็นความกว้างของแท่งสี่เหลี่ยมผืนผ้าสีขาวเพียง 1 แท่ง หรืออีกนัยหนึ่ง คือ “การกระจัดของวัตถุเพียงส่วนเดียวเท่านั้น” ดังนั้น “การกระจัดทั้งหมด $D_{total} = n\Delta{D}$ นั่นเอง

จากสมการที่ 1 จะสามารถเขียนงานในอีกรูปแบบได้ดังนี้ โดยการคูณเศษส่วน n/n ลงไป

$W_{total} = \frac{(F_1 + F_2 + F_3 + ... + F_n)}{n} \times (n\Delta{D})$

แต่เนื่องจากเรากำหนดไว้แล้วว่า $D_{total} = n\Delta{D}$ ดังนั้นจะได้ว่างานทั้งหมดสำหรับกรณีแรงไม่คงที่ คือ

$W_{total} = \frac{(F_1 + F_2 + F_3 + ... + F_n)}{n} \times (D_{total})$

หรือ

$W_{total} = \overline{F} \times (D_{total})$

โดยที่

$W$ คือ งานทั้งหมด ในหน่วยจูล (J)
$\overline{F}$ คือ แรงเฉลี่ย หรือเทอม $\frac{(F_1 + F_2 + F_3 + ... + F_n)}{n}$ ในหน่วยนิวตัน (N)
$D_{total}$ คือ ขนาดของการกระจัดทั้งหมดที่วัตถุเคลื่อนที่ได้ ในหน่วย เมตร (m)