การเคลื่อนที่แบบวงกลมหมุนแบบกรวย

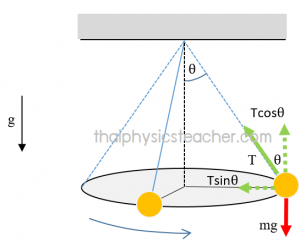
สมการการเคลื่อนที่แบบวงกลมหมุนแบบกรวย

เมื่อนำวัตถุมวล m มาผูกด้วยเชือก แล้วแกว่งในแนวระดับจนกระทั่งมีลักษณะเป็นรูปกรวย (ดังรูปข้างบน) วัตถุจะเคลื่อนที่แบบวงกลมในแนวระดับ เมื่อพิจารณาแรงที่กระทำกับวัตถุ พบว่ามีแรงเนื่องจากน้ำหนัก mg และแรงตึงเชือก T

เนื่องจากเชือกทำมุม $\theta$ กับแนวดิ่ง ทำให้เราสามารถแตกแรงตึงเชือก T ได้สองแนว กล่าวคือ แนวดิ่งจะมีแรงตึงเชือก $Tcos\theta$ กระทำกับวัตถุในแนวดิ่ง และแรงตึงเชือก $Tsin\theta$ กระทำกับวัตถุในแนวระดับ โดยที่แรงตึงเชือกนี้จะทำหน้าที่เป็นแรงเข้าสู่ศูนย์กลาง $m\frac{v^2}{R}$

พิจารณาแรงที่กระทำกับวัตถุในแนวดิ่ง พบว่าวัตถุไม่มีการเคลื่อนที่ขึ้นลงในแนวดิ่ง แสดงว่า

$\Sigma F = 0$

$Tcos\theta - mg =0$

$Tcos\theta = mg$ — (1)

พิจารณแรงที่กระทำกับวัตถุในแนวระดับ พบว่าวัตถุเคลื่อนที่เป็นวงกลมได้ แสดงว่าแรง $Tsin\theta$ ทำหน้าที่เป็นแรงเข้าสู่ศูนย์กลาง

$Tsin\theta = m\frac{v^2}{R}$ —(2)

นำสมการ (2) / (1) จะได้ว่า

$tan\theta = \frac{v^2}{Rg}$

แสดงว่ามุมของการเคลื่อนที่นี้มีค่าขึ้นอยู่กับความเร็ว v และรัศมีการเคลื่อนที่ R โดยที่ g เป็นค่าคงที่

Related posts:

ตรวจพบ Ad Blocker