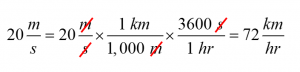เนื้อหา :
สมการทางฟิสิกส์สำคัญอย่างไร
ในทางฟิสิกส์เราใช้สมการเพื่อแสดงความสัมพันธ์ ซึ่งเหมือนเป็นตัวแทนปริมาณต่างๆในเหตุการณ์ที่เราสนใจ หากเปรียบเทียบเหตุการณ์ในชีวิตประจำวันที่ประกอบไปด้วย บุคคลที่ 1 บุคคลที่ 2 เวลา สถานที่ เป็นต้น ก็คงเหมือนเหตุการณ์ในทางฟิสิกส์ที่เรามักจะกล่าวถึง มวล เวลา การเคลื่อนที่ ตำแหน่ง เช่นกัน หากชื่อบุคคล ชื่อสถานที่เป็นชื่อเรียกส่วนประกอบของเหตุการณ์นั้นๆฉันใด ชื่อตัวแปรต่างๆในสมการก็เป็นแค่ตัวแทนในการนำมาพิจารณาความสัมพันธ์ทางฟิสิกส์เช่นกัน
การระบุค่าปริมาณทางฟิสิกส์
เราใช้สัญลักษณ์พีชคณิตแทนปริมาณทั้งตัวเลขและหน่วย เช่น d อาจแทนระยะทาง 25 m (จะเห็นว่าแทนด้วยตัวอักษรทั้ง ชื่อปริมาณ “d” แทนตัวเลขเพื่อระบุค่าปริมาณ และตัวอักษร “m” แทนหน่วยของปริมาณนั้นๆ) เป็นต้น โดยสรุปแล้วการบอกค่าปริมาณใดๆทางฟิสิกส์จำเป็นต้องระบุสิ่งที่ควรระบุดังนี้ 1. ชื่อปริมาณ 2. ค่าของปริมาณ 3. หน่วยของปริมาณ ถึงจะครบถ้วนสมบูรณ์และก่อให้เกิดความหมาย
ความสอดคล้องเชิงมิติ
สมการทุกสมการจะต้องมีความสอดคล้องเชิงมิติเสมอ พูดให้เข้าใจง่ายๆคือ หากมีดินสอ 1 แท่ง นำมาบวกกับรถยนต์ 5,000 กิโลกรัม ไม่ได้ เพราะหน่วยของปริมาณทั้งสองไม่เหมือนกัน (กล่าวคือเป็นปริมาณต่างมิติกัน จึงเรียกว่า ไม่มีความสอดคล้องในมิติ) ลองดูความสัมพันธ์ของสมการอย่างง่ายนี้ เพื่อตรวจสอบความเข้าใจกันครับ
s = vt
โดยที่ s แทนปริมาณระยะทางมีหน่วยเป็น เมตร (m)
v แทนปริมาณอัตราเร็วมีหน่วยเป็น เมตรต่อวินาที (m/s)
t แทนปริมาณเวลามีหน่วยเป็น วินาที (s)
การตรวจสอบความสอดคล้องเชิงมิติของสมการ
เวลาพิจารณาความสอดคล้องเชิงมิติ ให้คิดง่ายๆว่า สองข้างของสมการ ต้องมีหน่วยเหมือนกัน
ด้านซ้ายของสมการมีหน่วยเป็น “เมตร (m)”
ด้านขวาของสมการมีหน่วยที่เกิดจากการคูณระหว่างปริมาณอัตราเร็วกับเวลา สุดท้ายจะได้หน่วยเป็น (เมตร/วินาที)*(วินาที) = เมตร
แสดงว่าสมการนี้มีมีความสอดคล้องเชิงมิติ (ภาษาบ้านๆ ผมขอเรียกว่า “สมการไม่ได้สร้างขึ้นมามั่วๆ” นั่นเองครับ)
แน่นอนว่าสมการทางฟิสิกส์ที่ใช้อธิบายปรากฏการณ์ต่างๆได้จริง ทุกสมการที่มีอยู่บนโลกใบนี้ ก็ล้วนมีความสอดคล้องเชิงมิติทั้งนั้น
การแปลงหน่วยของปริมาณต่างๆ
การแปลงหน่วย คืออะไร ยกตัวอย่างเช่น อัตราเร็วในทางฟิสิกส์จะนิยมใช้หน่วย SI คือ 20 เมตรต่อวินาที (m/s) แต่ในชีวิตประจำวันเราจะรู้สึกตีความได้ยากว่า 20 เมตรต่อวินาทีนั้น เร็วเพียงใด เพราะความคุ้นเคยกับหน่วย กิโลเมตรต่อชั่วโมง (km/hr) ฉะนั้นการแปลงหน่วยจาก m/s ไปเป็น km/hr หรือหน่วยของปริมาณใดๆก็ตาม กระทำเพื่อความคุ้นเคยในการตีความนั่นเอง
การแปลงหน่วยในแต่ละครั้งจะอาศัยความสอดคล้องเชิงมิติและการแปลงคำอุปสรรค ช่วยพิจารณา ดังนี้
“ต้องการแปลงจาก 20 เมตรต่อวินาที ให้เป็นหน่วย km/hr”
จะเห็นว่า เราใช้คำอุปสรรค ต่างๆที่จำเป็น ดังนี้ 1 km = 1,000 m และ 1 ชั่วโมง = 3,600 วินาที แล้วนำไปเทียบเพื่อตัดหน่วยที่ไม่ต้องการออก (ในทีนี้คือ m และ s) ให้เหลือหน่วย km/hr ตามต้องการ ซึ่งสุดท้ายจะได้ข้อสรุปว่า “20 m/s = 72 km/hr” ทีนี้เราก็จินตนาการออกได้ว่าอัตราเร็วนี้ก็เร็วๆพอกับรถยนต์ที่ขับในถนนปกติเลยครับ