การต่อตัวต้านทานแบบอนุกรม

การต่อตัวต้านทานแบบอนุกรม (Resistors in Series) จะต่อกันดังรูปด้านล่าง

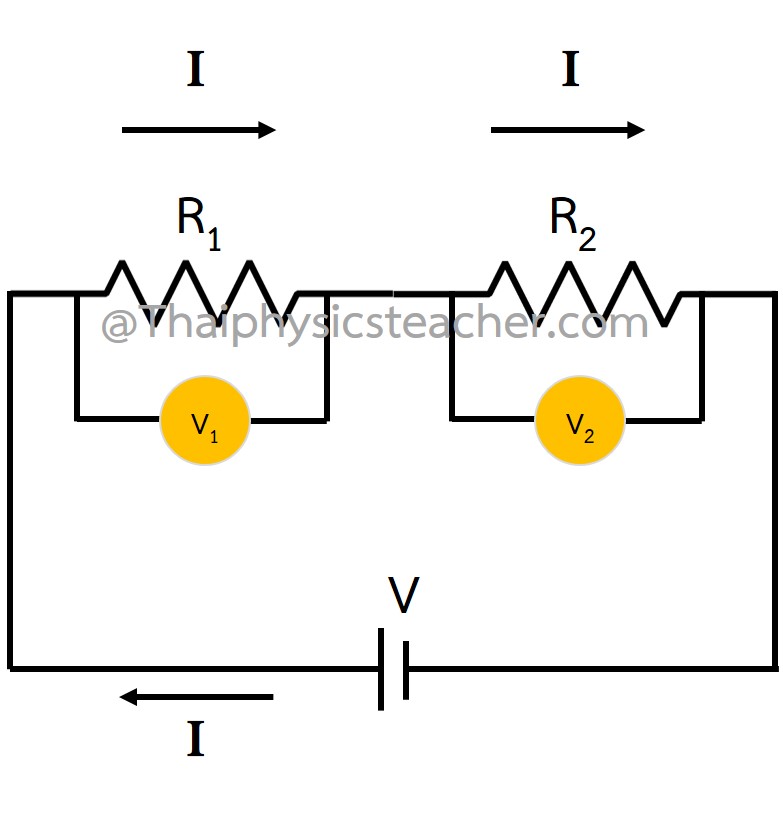
เมื่อนำโวลต์มิเตอร์ไปต่อตกคร่อมตัวต้านทานที่มีความต้านทาน $R_1$ และ $R_2$ ตามลำดับ พบว่าความต่างศักย์ตกคร่อมจะมีค่าไม่เท่ากัน คือ $V_1$ และ $V_2$ ตามลำดับ

แต่ผลรวมความต่างศักย์ตกคร่อมตัวต้านทานแต่ละตัวจะเท่ากับความต่างศักย์ตกคร่อมของถ่านไฟฉาย ถ้าถือว่าไม่มีความต้านทานภายในของถ่านไฟฉาย และไม่มีการสูญเสียพลังงานไฟฟ้าไปกับพลังงานรูปแบบอื่น จะได้สมการ ดังนี้

$V_{total} = V_1 + V_2 --- (1)$

และเมื่อกระแสไฟฟ้าไหลครบวงจร ก็พบว่ากระแสไฟฟ้าที่ไหลผ่านตัวต้านทานจะมีขนาดเท่ากัน เปรียบเสมือนน้ำที่ไหลผ่านท่อเดียวกันจะมีอัตราการไหลเท่ากัน ดังนั้นเราจะได้ความสัมพันธ์ ดังสมการ

$I_{total} = I_1 = I_2 --- (2)$

จากกฎของโอห์ม V = IR นำไปแทนค่าในสมการที่ 1 จะได้

$(I_{total})(R_{total}) = (I_1)(R_1) + (I_2)(R_2)$

และจากความสัมพันธ์สมการที่ 2 จะสามารถหารด้วยเทอมของกระแสไฟฟ้าออกทั้งสองข้างได้ ดังนี้

$R_{total} = R_1 + R_2$

นั่นแสดงว่าความต้านทานรวมของตัวต้านทานที่นำมาต่อแบบอนุกรมกัน จะมีค่าเท่ากับผลรวมของความต้านทานย่อย ถ้ามีตัวต้านทาน n ตัว ที่มีขนาดไม่เท่ากัน เมื่อนำมาต่อแบบอนุกรมจะได้ความต้านทานรวม ดังสมการนี้

$R_{total} = R_1 + R_2 + R_3 + ... + R_n$

Previous Page: ความแตกต่างระหว่าง “แรงดันไฟฟ้า” กับ “ความต่างศักย์ไฟฟ้า”

Next Page: การต่อตัวต้านทานแบบขนาน

Related posts:

ตรวจพบ Ad Blocker